SISTEMES D'EQUACIONS LINEALS (Apunts necessaris vàries activitats)
3. Mètodes de resolució d'un sistema d'equacions lineals
3.3. Mètode de reducció
Els passos que cal seguir per resoldre un sistema pel Mètode de reducció són els següents:
- Es multiplica cada equació per un nombre (positiu o negatiu) per aconseguir el mateix coeficient en una de les incògnites, llevat dels signes, que es deixen diferents.
- Se sumen les dues equacions del sistema per obtenir així, una equació amb una incògnita.
- Es resol l'equació (amb una sola incògnita) obtinguda.
- Es calcula el valor de l'altra incògnita i se substitueix en una de les dues equacions del sistema.
- Es comprova que els valors obtinguts de les incògnites x i y són la solució del sistema d'equacions.
EXEMPLE:
En aquest cas, multipliquem la primera equació per 1 i la segona per 2
ALTRES EXEMPLES RESOLTS:
A continuació podeu veure uns quants exemples resolts. Per veure la solució a
tan sols cal clicar damunt de cada sistema d'equacions:
 |
 |
 |
 |
 |
 |
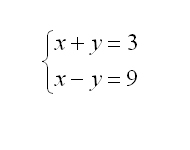
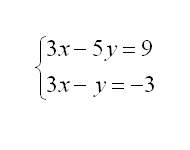
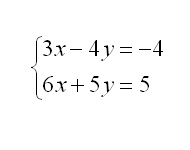
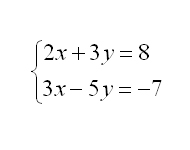
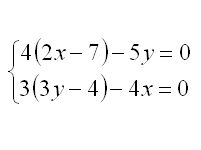
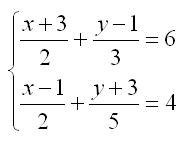